Contenu des cours
L'échantillonnage et l'estimation apportent des solutions à deux problèmes différents mais qu'il est facile de confondre.
Les documents ci-dessous doivent vous permettre de mieux cerner les problématiques et d'éviter les confusions.
- Activité 1 page 232
- Lien vers la correction des questions 1 et 3 de l'activité.
- Vidéo : correction de la question 2
- Partie échantillonnage
- Echantillonnage : lire le cours page 236 - voir l'exercice résolu page 237
- Vidéo : Pouquoi faut-il respecter des critères de normalité ?
Les critères de normalité sont donnés dans un encart bleu de la page 236, on voit dans l'exercice résolu de la page 237, qu'avant de déterminer un intervalle de fluctuation, la première chose à faire était de vérifier que ces critères sont bien respectées. Mais pourquoi ?
- Vidéo : D'où viennent les formules de calcul
des bornes de l'intervalle de fluctuation ?
L'explication ci-dessous prend comme contexte celui de l'activité 1 page 232.
- Vidéo : Décider à partir de la fréquence d'un échantillon
L'explication ci-dessous prend comme contexte celui de l'activité 1 page 232. On affirme que 20 % des meringues sont cassées. A partir de la fréquence de meringues cassées dans un échantillon, que peut-on dire de cette affirmation ?
- Prendre une décision à partir de la fréquence d'un échantillon : lire le cours page 238 - voir l'exercice résolu page 239 Planche de représentations graphiques de la fonction de Gauss..
- Partie estimation
- Estimer une proportion inconnue, intervalle de confiance: lire le cours page 240 - voir l'exercice résolu page 241
- Partie échantillonnage
- Méthode : déterminer un intervalle de fluctuation
- Intervalle de fluctuation : exercice 1 page 237
- Intervalle de fluctuation : exercices 19 et 20 page 244
L'exercice 19 est corrigé dans le livre à la page 278
Lien vers la correction du 20 page 244. - Décider à partir de la fréquence d'un échantillon : exercices 3 page 239
- Décider à partir de la fréquence d'un échantillon : exercices 22 et 23 page 245
L'exercice 22 est corrigé dans le livre à la page 278
Lien vers la correction du 23 page 245. - Décider à partir de la fréquence d'un échantillon : exercice 54 page 256
- Partie estimation
- Méthode : estimer une proportion avec un intervalle de confiance.
- Calculer un intervalle de confiance : exercice 5 page 241
- Calculer un intervalle de confiance : exercice 28 page 246
- Méthode : déterminer la taille d'un échantillon.
Plus la taille de l'échantillon est importante, plus l'intervalle de confiance sera petit et donc plus la précision sur la valeur de la proportion sera grande. Mais en général prendre un grand échantillon coûte cher, voilà pourquoi il est intéressant de déterminer au plus juste la taille nécessaire.
Lien vers une vidéo d'Yvan Monka. - Déterminer la taille d'un échantillon :
exercice 29 page 246
L'exercice est corrigé à la page 278
Avant d'aborder les lois de probabilités à densité, j'ai souhaité faire un retour sur les notions d'expérience aléatoire et de variable aléatoire .
C'est l'occasion également de refaire le point sur la notion d'espérance d'une variable aléatoire.
- Espérance et moyenne
Lorsqu'on répète une expérience aléatoire un grand nombre de fois, les fréquences observées des valeurs prises par une variable aléatoire se rapprochent des probabilités de ces valeurs.
Comme la somme de ces probabilités est égale à 1, on peut voir l'espérance d'une variable aléatoire comme la valeur moyenne de cette variable quand on répète l'expérience un grand nombre de fois.
Les propriétés mathématiques de l'espérance sont donc celles d'une moyenne. C'est ce que mettent en avant les exercices 45 et 46 page 192.
Pensez à retourner à cette page et à lire les encadrés violets lorsque vous rencontrez des difficultés concernant l'espérance.
- Expérience aléatoire et variable aléatoire
"Lancer un dé tétraédrique dont les faces sont numérotées de 1 à 4 et noter la face qui apparaît" est une expérience aléatoire
Les issues de cette expérience sont "1" ; "2" ; "3" ; "4".A cette expérience aléatoire, on peut associer une variable aléatoire, par exemple la variable aléatoire peut prendre la valeur 1 si le nombre "4" apparaît, la valeur -1 si le nombre "1" apparaît et 0 dans les autres cas.
Mais on peut avec la même expérience aléatoire définir d'autres variables aléatoires . C'est ce que nous avons fait ensemble mardi.
Attention cela ne correspond pas tout à fait à l'exercice C page 172 car nous avons considéré que nous lancions le dé qu'une seule fois.Lien vers le travail de mardi : plusieurs variables aléatoires pour une même expérience aléatoire.
Pour la correction du C page 172 voir en bas de la page 329
- Représentations graphiques
Représentation loi de probabilité discrète et loi binomiale.
La première fiche d'exercices revient sur la représentation d'une loi de probabilité discrète et sur l'analyse de la représentation d'une loi binomiale.
Lien vers la fiche
Lien vers la correction du premier exercice
Lien vers la correction du deuxième exercice
Lien vers un utilitaire géogébra pour la représentation de la loi binomiale.
Représentation d'une série statistique : histogramme.
Avant de passer aux lois à densité, il est nécessaire de revoir la représentation graphique d'une série statistique lorsque le caractère étudié est quantitatif et continu.C'est l'objet de l'activité qui suit.
Lien vers l'activité.
La correction de cette activité contient les principes de construction d'un histogramme qui permet de représenter la répartition d'une variable statistique continue.
Lien vers la correction de l'activité.
L'exercice 58 page 221 de votre livre fait travailler la construction d'histogramme.
- Activité
Le but de cette activité est de comprendre comment on peut construire un modèle pour calculer des probabilités dans le cas d'une variable aléatoire continue.
Nous allons partir d'une variable statistique continue et de la représentation de cette variable à l'aide d'un histogramme.
Lien vers l'activité.
-
Leçon : loi de probabilité à densité.
- Vidéo : leçon "Loi normale centrée, réduite".
Cette vidéo permet de compléter la partie "Loi normale, centrée, réduite.
- Vidéo : leçon "Loi normale".
Je n'ai pas pu tourner la vidéo. Allez voir le cours sur la loi normale à la page 210 de votre livre. J'expliquerai le contenu de la vidéo en visio.
Planche de représentations graphiques de la fonction de Gauss..
- Loi uniforme : exercices page 207
- Loi normale : activité d'approche.
Dans la correction, j'apporte des compléments sur le début de l'étude de la loi normale.
Lien vers la correction. - Loi normale, étude de la fonction de Gauss : 39 page 215

- Corrections 25 et 26 page 214
- Vidéo : correction du 33 page 215.
Attention une erreur à la question 1.c 0,15% = 0,0015 donc la probabilité est 0,0015
- Vidéo : correction du 35 page 215.
- Usage de la calculatrice.
Rendez vous sur le site d'Yvan Monka pour trouver les vidéos expliquant comment calculer une probabilité avec une loi normale.
- Méthode : exercice résolu loi normale.
- Corrections 49 et 50 page 219
La correction de ces exercices met en avant deux choses :
- L'interprétation graphique des probabilités calculées. Vous aurez tout le temps dans les années à venir de calculer des probabilités. Il est important en ce moment de vous forger de bonnes images mentales, de bonnes représentation de la loi normale. Ces interprétations y participent.
- L'utilisation des critères de normalité que vous trouverez en bas de la page 210. Le but est toujours de construire votre représentation de la loi normale et ici acquérir des ordres de grandeurs.
Deux erreurs sur le 45 en début de vidéo : je dis à plusieurs reprises 50 à la place de 150 et je note 150 minutes = 1 heure 30 minutes à la place de 2 heures 30 minutes.
- Correction 53 page 219
Un exemple de calcul à l'ancienne avec une table de probabilité, la calculatrice donne des résultats plus précis.
- Correction 66 page 225
Un bon exemple pour aborder la notion de faux-positif et faux-négatif qui n'a rien à voir avec les probabilités conditionnelles. Nous reviendrons sur cette notion en visio.
Par ailleurs, si 80% des cartes retournées avaient un défaut, cela veut dire que 20 % des cartes retournées étaient conformes. Choquant ou pas ?
A la fin de ce chapitre, vous devez être capable de calculer une primitive d'une fonction dans des cas simples.
Mais surtout vous devez avoir compris que "primitive- fonction" et "fonction-dérivée" sont deux façons d'exprimer le même lien.
Quand on demande de vérifier que F est une primitive de f, il est souvent plus simple de vérifier que f est la dérivée de F.
L'autre volet du chapitre concerne les intégrales. Pour cela il est indispensable que vous soyez bien au clair sur les notions d'aire et de mesures d'aires. Certes ces notions vous suivent depuis l'école primaire, mais elles ne sont pas simples.
Le chapitre se termine sur la notion de valeur moyenne d'une fonction continue sur un intervalle.
Les notions abordées dans ce chapitre seront réuntilisées aux moments de l'étude des lois de probabilités à densité.
- Vidéo : intégrales et primitives, à quoi ça sert ?
- Compléments vidéo : déterminer une aire sans primitives .
- Vidéo : exercices de base.
Ces exercices sont à faire à l'aide du tableau des dérivées.
Attention il y a des erreurs dans le tableau qui apparaît à l'écran. - Exercices 52 et 54 page 154

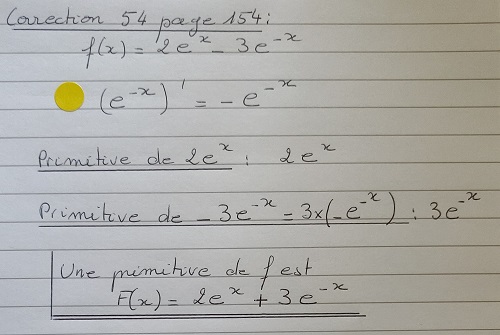
- Vidéo : primitive avec la fonction exponentielle.
- Exercice 59 page 154

- Vidéo : aires et mesures d'aires.
- Vidéo : description d'un domaine du plan.
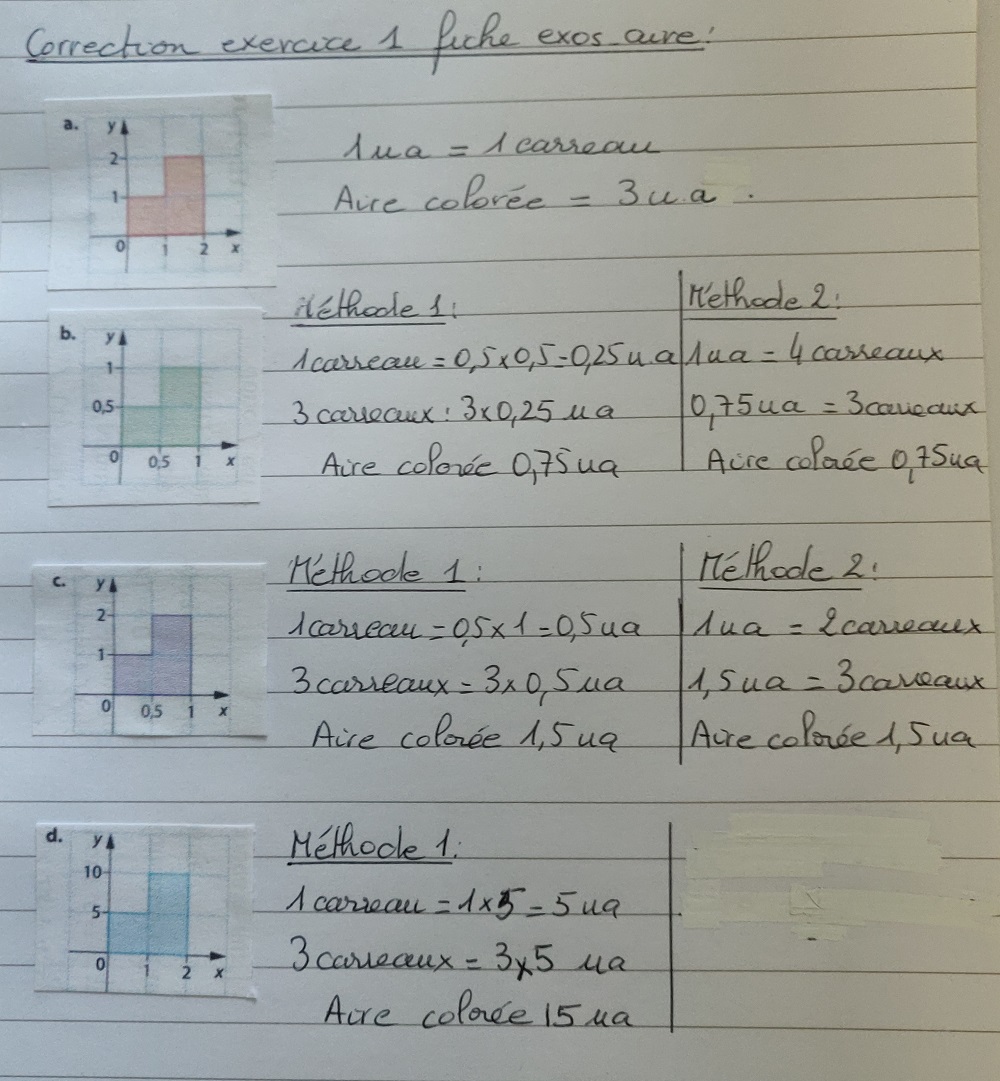
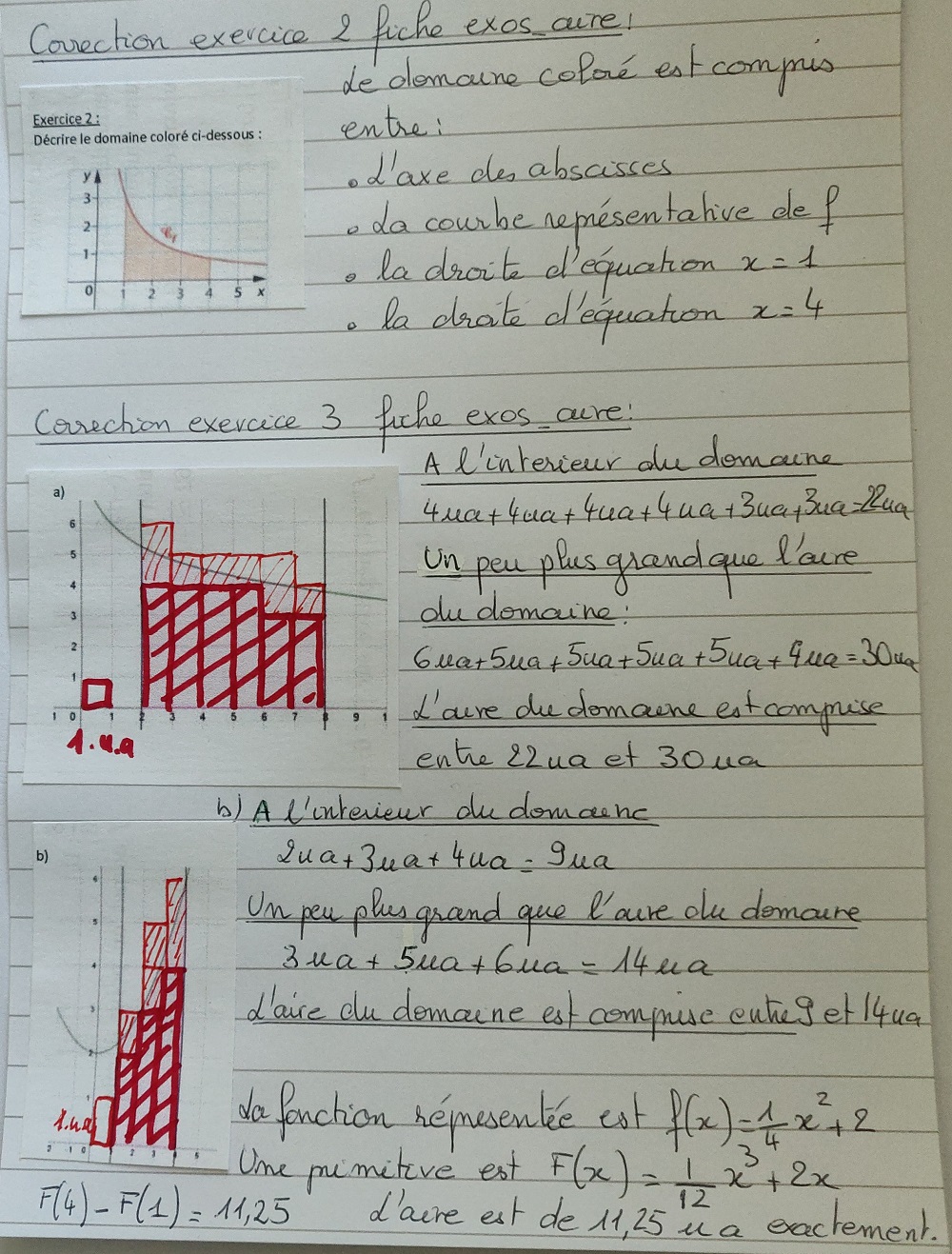
- Exercices sur les aires en préparation des intégrales.
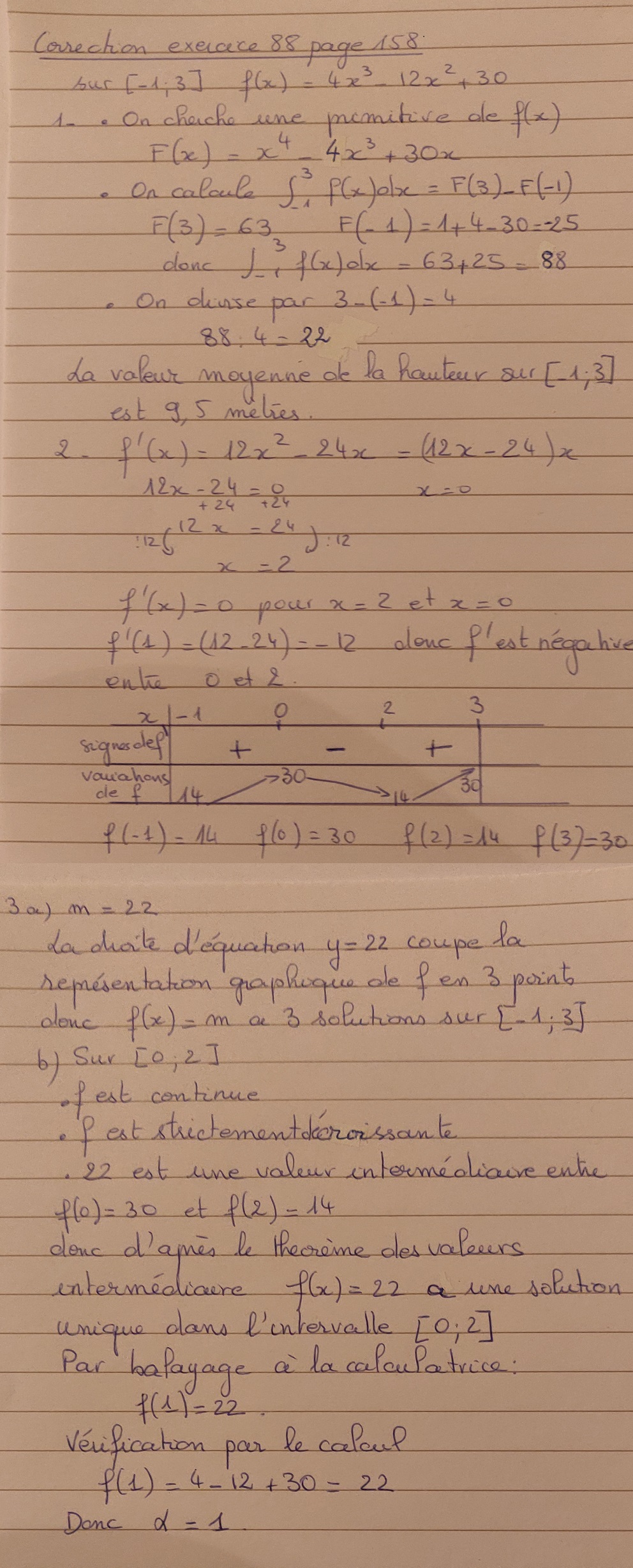
- Exercices 71 et 73 page 155


- Fiche d'exercices sur les primitives et intégrales.
Il s'agit essentiellement d'exercices de bac. L'idée est de retrouver ce que vous avez fait dans ce chapitre dans différents contextes.
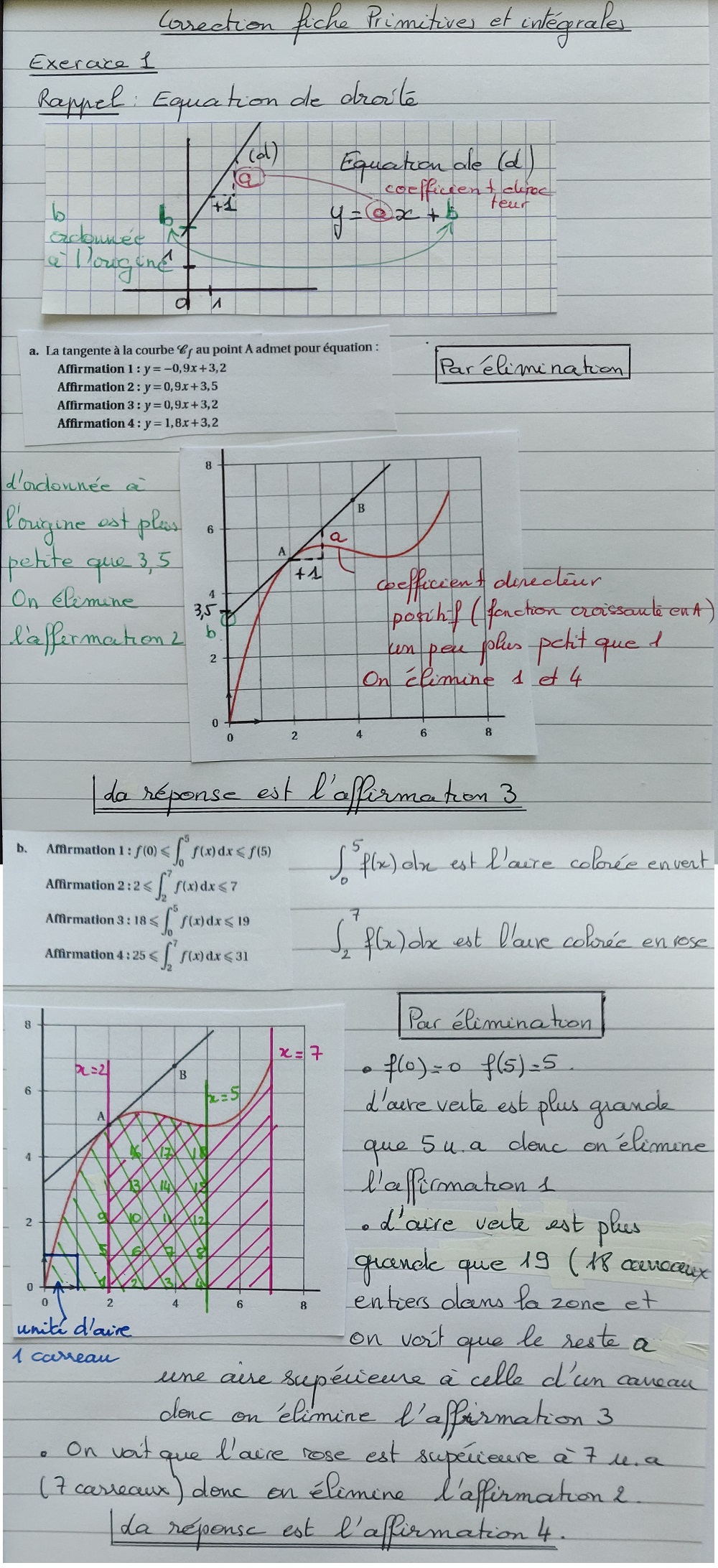
Lien vers la fiche d'exercices.Corrections :




- Vidéo : moyenne d'une fonction continue.
- Fiche d'exercices sur les moyennes.