Addition de deux nombres relatifs

Le modèle de la droite numérique est bien en place :

Nous avons multiplié les déplacements des nombres très grands vers des nombres très petits, des nombres très petits vers les nombres juste avant -1, par exemple -1,00001. Certains élèves ont tenté de relever le défi de s’approcher encore :
« Madame, moi je peux aller encore plus près : -1,000011
– Raté 🙂 »

Le doigt des élèves s’est aussi beaucoup déplacé sur la droite, de façon régulière sans marquer le passage à zéro éprouvant ainsi l’homogénéité d’une droite affine.

Le calcul de la longueur d’un segment est maitrisé lui-aussi :

Ceci, dans le contexte présenté dans le précédent article. De plus les élèves ont été entrainés aux additions et soustractions mentales, ce qui va être précieux pour la suite.

Voici venu le temps de l’introduction de l’addition de deux nombres relatifs.

Nous introduisons l’addition de deux nombres relatifs avec le modèle des déplacements, c’est un choix didactique.

En préambule, il faut remarquer qu’il y a deux façons de représenter une addition sur une droite numérique :

• Soit on ajoute un déplacement à une position et on obtient une position :
  Je suis en -3, j’avance de 4 vers la droite et j’arrive en 1 : -3+4=1
• Soit on se place en zéro, et on ajoute deux déplacements :
  Je  recule de 3 et j’avance de 4, c’est comme si j’avais avancé de 1

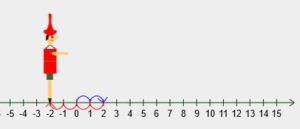
C’est la deuxième option que nous avons prise :

• Le personnage qui se déplace est orienté, c’est pourquoi nous avons choisi Pinocchio : il a un grand nez, de plus nous lui avons fait tendre le bras : il n’a pas d’ambiguïté sur le sens dans lequel il se trouve.
  
• On le place en 0, les nombres positifs codent un déplacement vers l’avant (avance), les nombres négatifs codent un déplacement vers l’arrière (recule) et le signe opératoire code une action du personnage entre les deux déplacements : + continue dans le même sens, – se retourne.
  

Avec le numérique ?

Cette option nécessite l’usage d’un outil numérique. En effet, c’est bien beau d’exposer le modèle, encore faut-il que les élèves le respectent :

• « Pour faire -3+4, je me mets direct à -3, ça va plus vite. 🙂 » Oui sauf qu’on change de modèle …
• « Mais non, madame, j’ai pas besoin de Playmobil©, je fais avec mon crayon . » Sauf que le crayon se déplace, il ne marque pas la distinction entre avancer et reculer! Dans l’interprétation des différents signes + et – ou au moment des soustractions, ça va poser problème.
• « Moi, je fais trois d’un coup : -2+3-1 », sauf que si le modèle le permet pour l’addition, cela ne va pas être possible pour la soustraction, mieux vaut donc bloquer la possibilité tout de suite.

Sur l’addition et la soustraction de deux nombres relatifs, nous sentions vraiment le besoin :

• de forcer le respect des règles du modèle d’une part,
• et de décharger les élèves d’une grande partie de l’apprentissage des règles du modèle pour qu’ils se concentrent sur l’apprentissage des additions et soustractions de deux relatifs.

Nous avons donc développer notre outil numérique :Pinocchio

Présentation rapide de l’outil :

Pour une présentation plus détaillée et une discussion sur l’outil voici le lien .

• Niveau 1 :  l’appropriation du modèle que je fais faire à tous les élèves. Certains passent trop vite dessus et il peut être nécessaire de les faire revenir sur ce niveau.
• Niveau 2 : les valeurs absolues des nombres sont petites, les résultats sont accessibles en « comptant ». L’élève peut faire afficher l’aide didactique et s’en servir pour trouver ou vérifier le résultat.
• Niveau 3 : la valeur absolue du deuxième terme est petite, donc les résultats sont toujours accessibles en comptant. Par contre la valeur absolue du premier terme est grande donc le résultat n’est pas toujours sur la portion de droite représentée, l’élève doit extrapoler.
• Niveau 4: Les valeurs absolues des nombres peuvent être grande, le passage à l’opération est souvent impératif. Trois aides sont proposées : une pour trouver le signe du résultat, une pour trouver « l’opération » à effectuer, et une calculatrice permet de faire des calculs, mais uniquement les additions de nombres positifs et les soustractions de nombres positifs quand le premier terme et supérieur au second.

Les niveaux suivants concernent les soustractions.

Les séries comportent 10 questions (5 pour le niveau 1). A la fin de la série, un tableau récapitulatif est affiché :

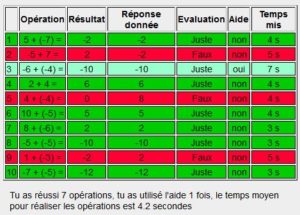
Il permet une analyse du travail de l’élève. Les résultats justes sont en vert (vert clair quand l’élève a utilisé l’aide de Pinocchio), les résultats faux en rouge (c’est pas un bon plan cette couleur, il faut que je la change).
Il est possible de voir les erreurs de signe, les erreurs d’opérations et les erreurs de calcul.
Le temps moyen pour réaliser les opérations permet aux plus rapides de faire la course et ainsi d’augmenter leurs compétences en calcul mental.

En pratique :

Du point de vue pratique, l’usage de Pinocchio nécessite le déplacement en salle informatique, sauf si on a la chance d’avoir des tablettes et internet. Une heure d’addition de relatifs, ce n’est pas possible. Donc je couple en général les séances avec des séances tableur et le chapitre sur les statistiques.

D’autre part certains élèves n’ont pas besoin de modèle pour additionner deux relatifs et d’autres vont s’affranchir très vite de celui-ci. L’outil permet de différencier les usages et donc de travailler sans modèle.

La mise en commun et l’institutionnalisation :

La mise en commun n’est pas facile à mettre en œuvre lors d’un travail en salle informatique avec des élèves :

• qui, pour certains peinent à s’approprier le modèle des déplacements,
• pour d’autres qui n’ont pas besoin du modèle,
• pour d’autres qui, parce qu’ils ont réussi le niveau 4 en moins de 5 secondes par opération, sont en train d’annoncer à tout le monde qu’ils sont les rois du pétrole,:) 🙂
• pour d’autres qui sont déjà passés sur tableur
• et pour d’autres enfin qui sont occupés à modifier mon code source : « Y a un problème , madame, ça m’affiche tout juste alors que j’ai faux 🙂  » Merci les compétences multiples.

Avec  un dispositif pédagogique qui permet de passer du temps individuellement avec chaque élève, la mise en commun est-elle nécessaire ?
Je n’en suis passée un an ou deux avant de trouver ma réponse à la question, c’est oui.

Mais comment faire? Pour ma part, je fais faire quelques calculs (entre 3 et 5) en début d’heure devant la classe entière. Je les corrige systématiquement avec Pinocchio pour favoriser l’appropriation du modèle chez les élèves qui sont encore en difficulté, et je laisse exposer différentes stratégies de calcul par les élèves, par exemple « Vu qu’il recule de 6 et qu’après il recule de 8, moi je fais 6+8  »
Ce moment permet aussi à certains de verbaliser leur interrogation sur le signe opératoire « Mais, le + entre les deux, il sert à quoi ? ».
Le mot « pas » peut être utilisé dans certains échanges : « 5 pas en avant et 6  pas en arrière, c’est comme s’il avait fait un pas en arrière. »

Quand à l’institutionnalisation, il n’y a que des exemples dans les cahiers de leçons de mes élèves. En effet, la verbalisation de procédures calculatoires est difficile et à mon avis contre-productive dans la mesure où chacun développe ses propres procédures :

De plus pour calculer -10+15, il est plus judicieux de faire « -10 et 10 pour aller à 0 et encore 5, soit 5 » c’est à dire de décomposer les déplacements.

Nous avons bien travailler 🙂 .  Maintenant on met le tout au frigo enfin de laisser le temps à la pâte de bien lever.
La semaine prochaine : à la découverte du frigo 🙂 .

N’hésitez pas à commenter, à exprimer vos points de désaccord ou votre point de vue, à demander des précisions.