Contenu des cours
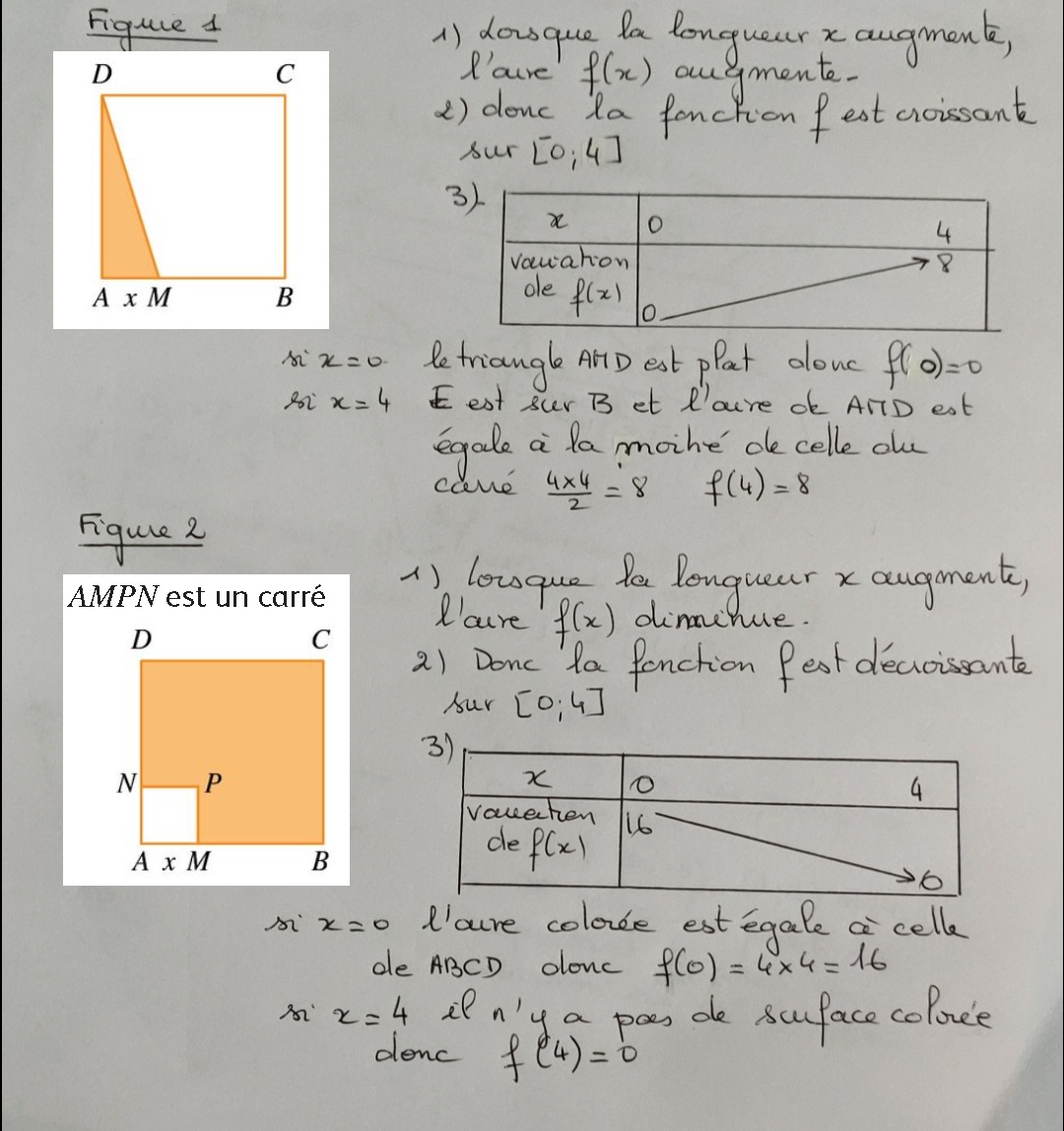
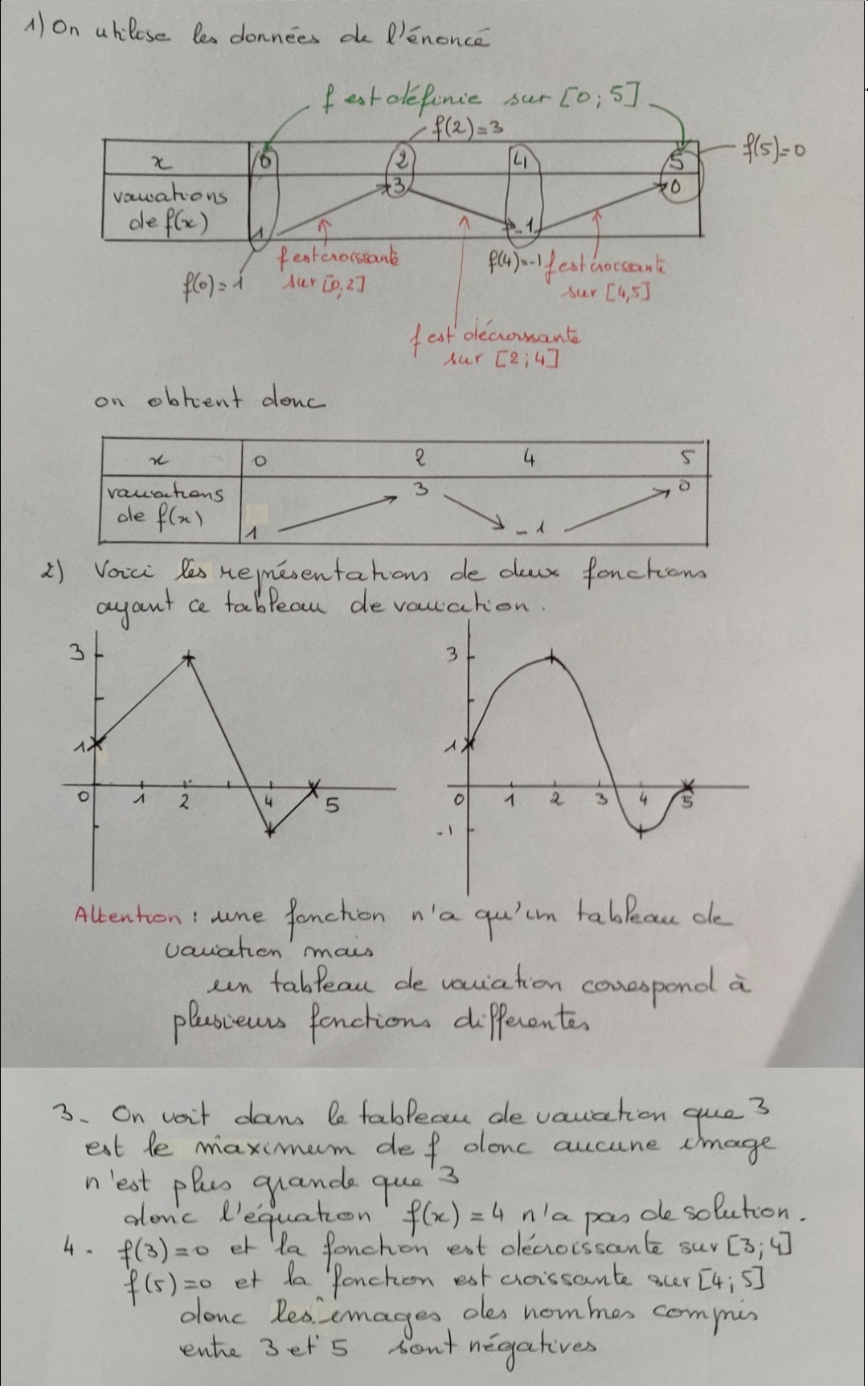
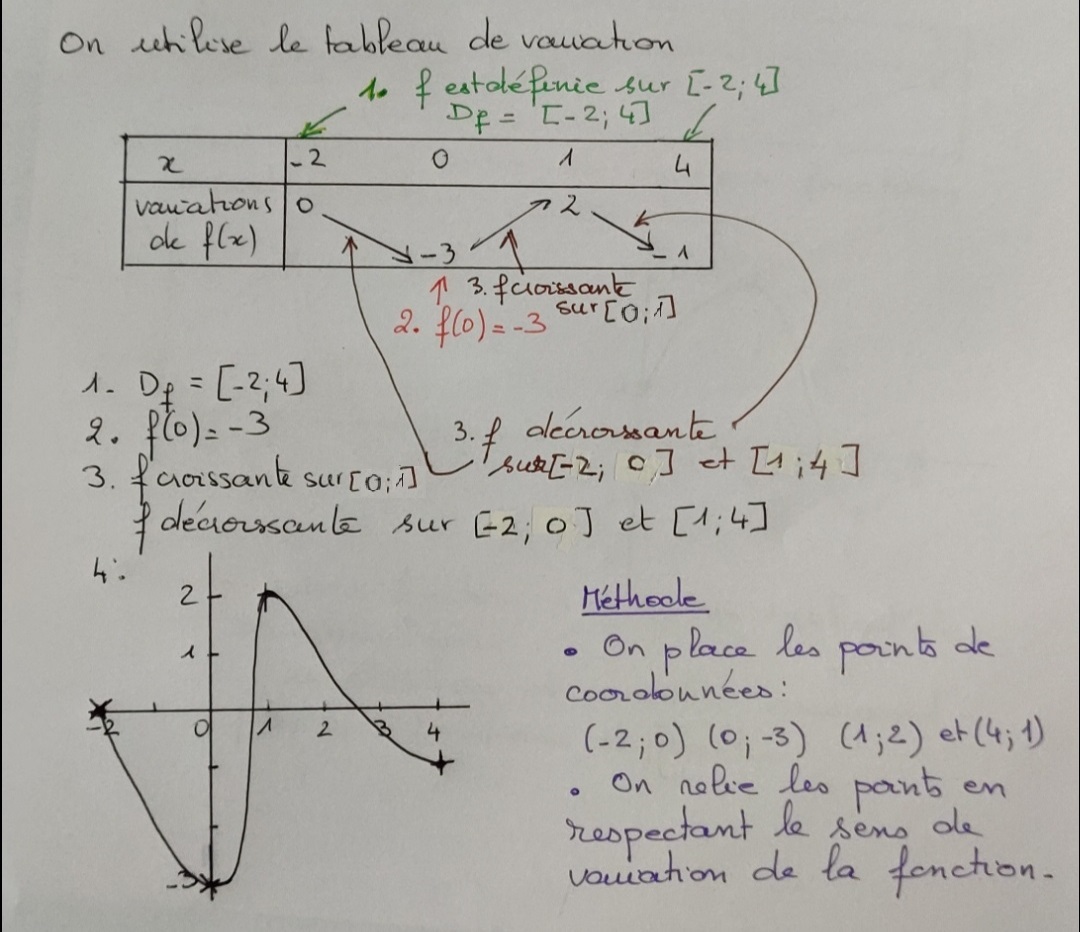
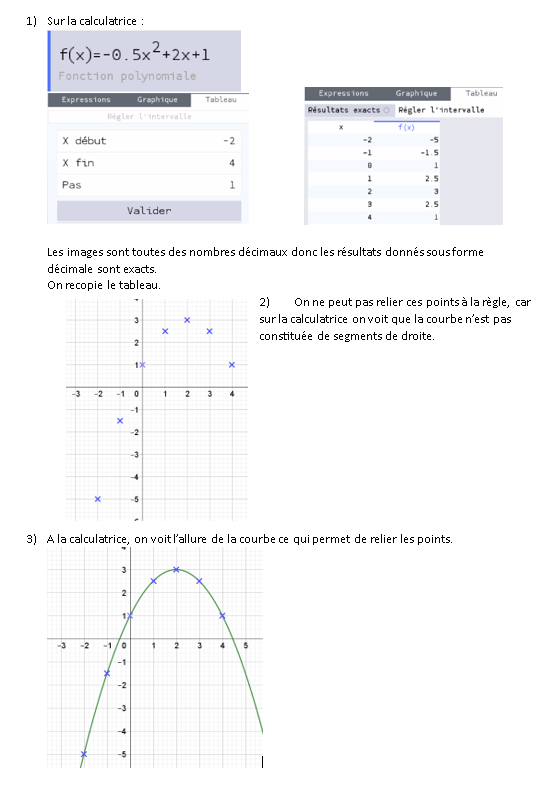
Correction de l'exercice 65 page 170
Correction de la partie A du Vrai-Faux page 170
Correction de l'exercice 50 page 174
Correction de l'exercice 40 page 173
Correction de l'exercice 41 page 173
Correction de l'exercice 53 page 174
Correction de l'exercice 39 page 173
Correction de l'exercice 35 page 172
Correction de l'exercice 33 page 172
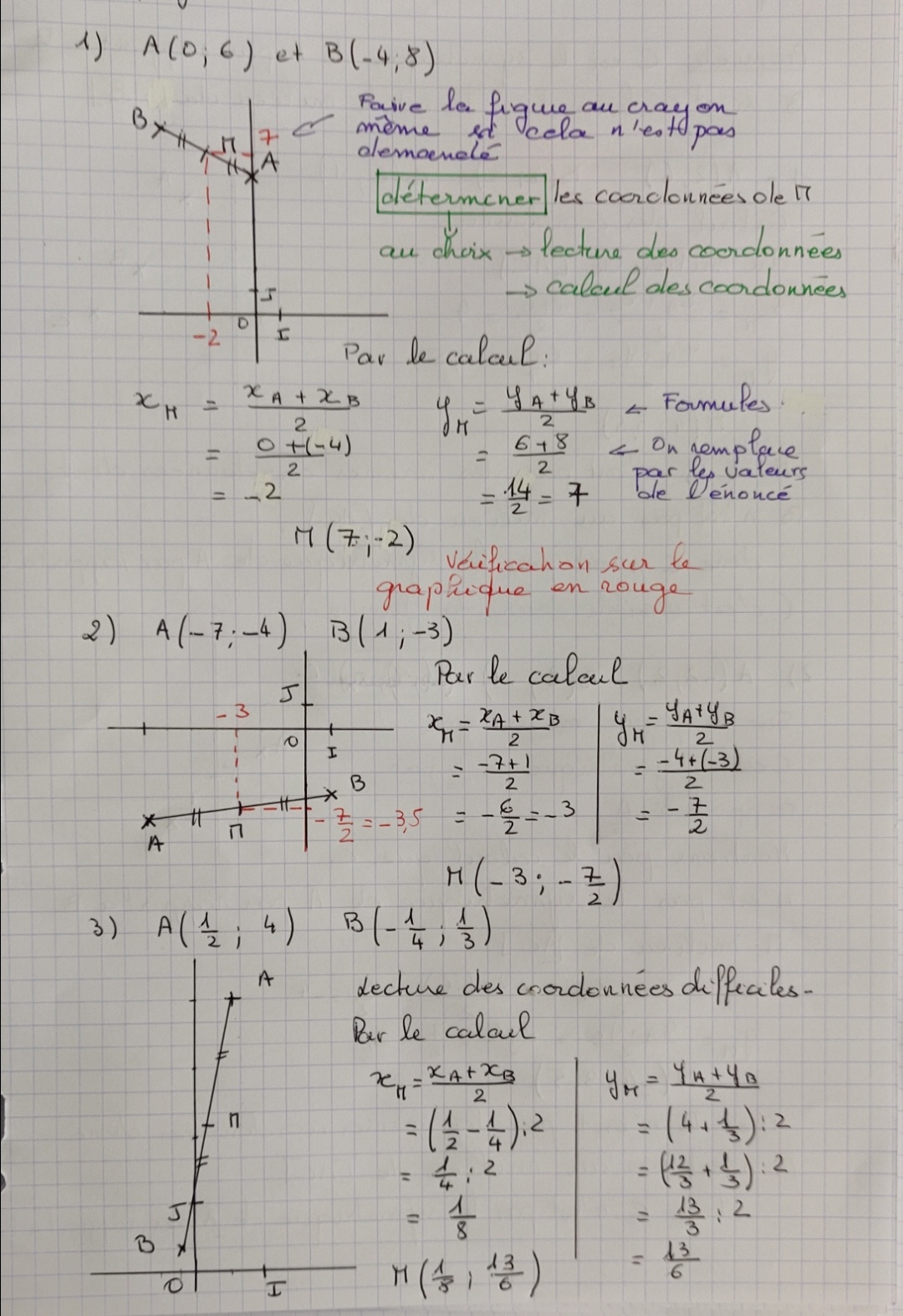
Correction de l'exercice 129 page 87
Equations de quotient nul : correction de
l'exercice 88 page 83
Factoriser pour résoudre une équation de produit
nul : correction de l'exercice 74 page 81
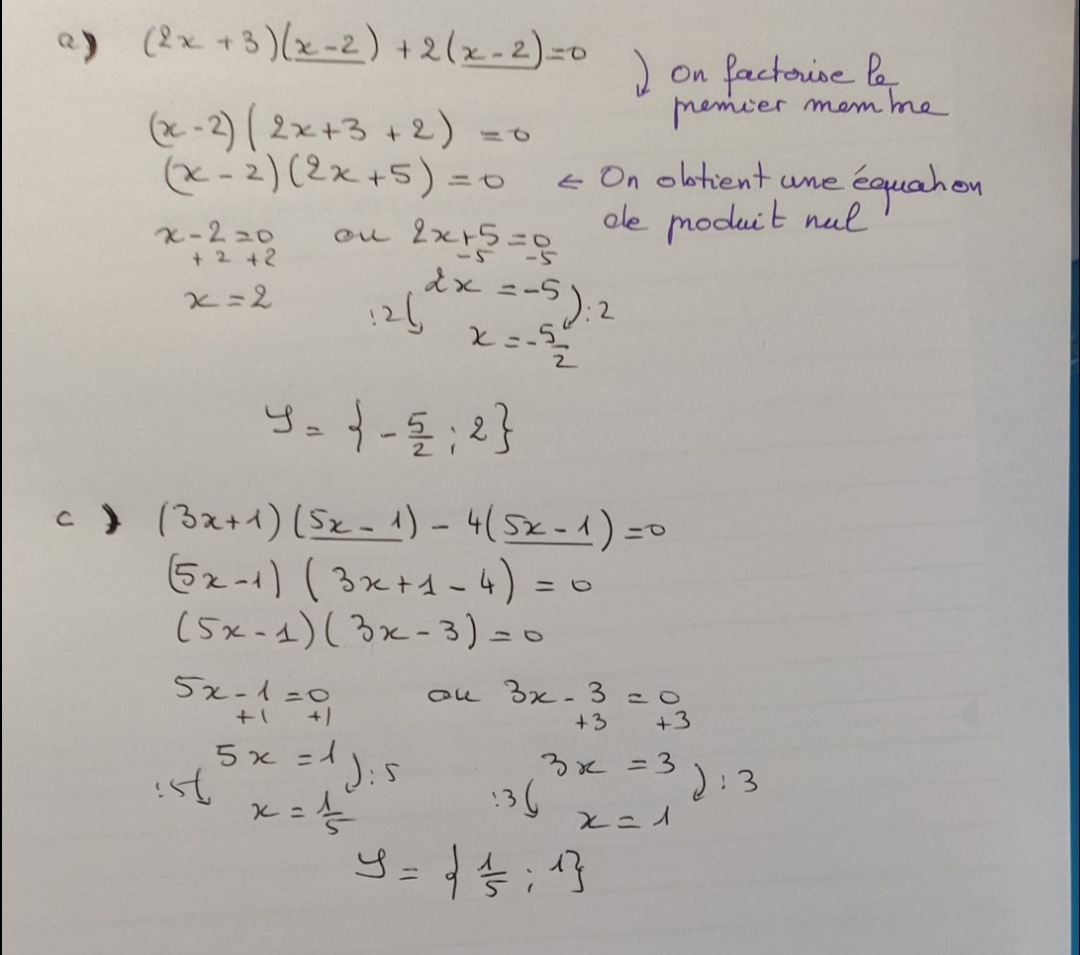
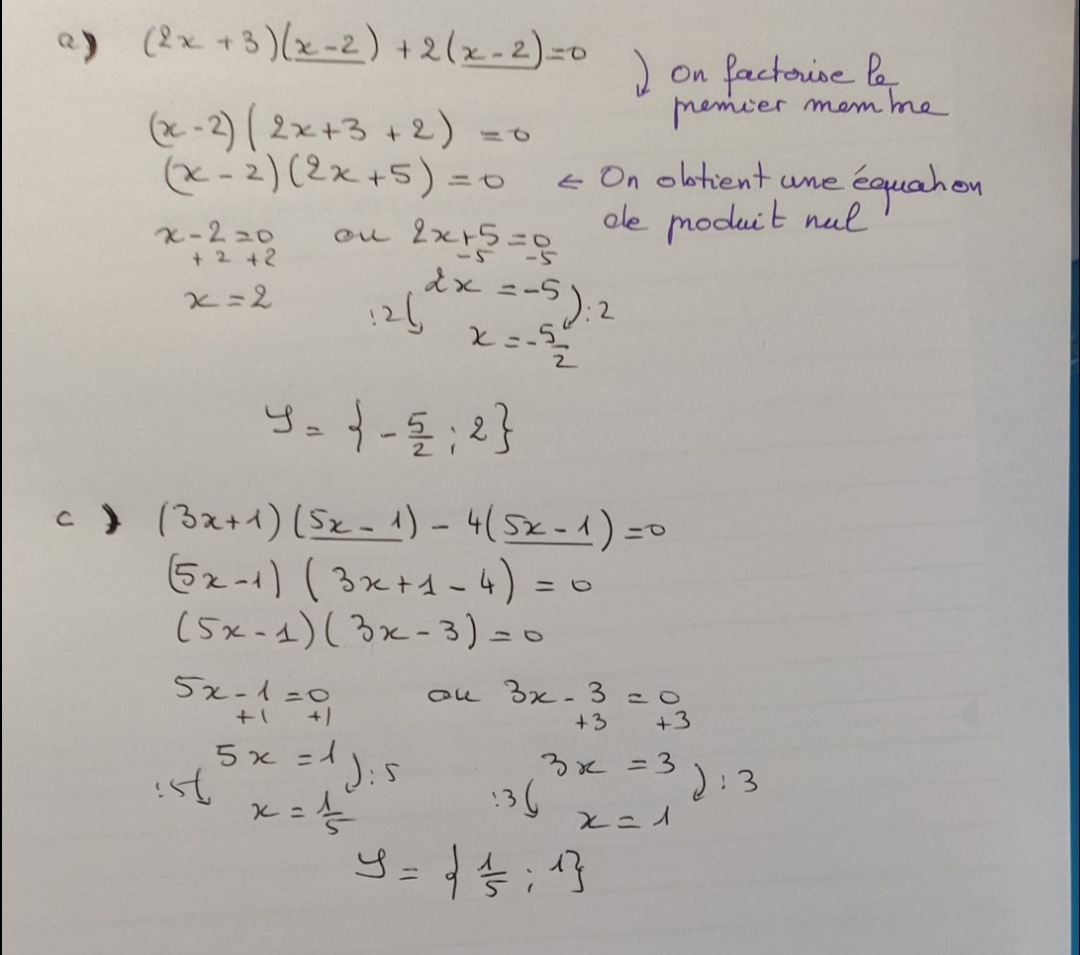
Equation de produit nul : correction de
l'exercice 72 page 81
Développer pour résoudre : correction de
l'exercice 71 page 80
Mise en équation : correction de l'exercice 95
page 83
Exercices de mise en équation
Correction de l'exercice 109 page 85
Valeurs interdites : correction de l'exercice 16
page 74
Développements et factorisations
Correction de l'exercice 56 page 80
Correction de l'activité 3
Fiche d'activités
Les activités sont en partie haute de la fiche.
Lien vers la fiche d'activitésCorrection de l'exercice 111 page 85
Enoncés et correction des exercices dictés
Exercice 1 :
Exercice 2 :
Exercice 3 :
Correction de
l'exercice 120 page 149
Correction 105 page 148
Correction 103 page 148
Correction 96 page 147 : relation de Chasles
Correction 101 page 147 : résolution de
problèmes
avec les vecteurs
Correction 89 page 146 : définition d'un
vecteur, vecteurs égaux
Correction 88 page 146 : vecteurs égaux
Correction 7 page 133 : construction de sommes
de vecteurs
Correction 4 page 133 : construction de sommes
de vecteurs
Je n'ai pas placé le point O, en effet dans cet exercice, on peut rester dans le plan vectoriel, pas besoin des points.
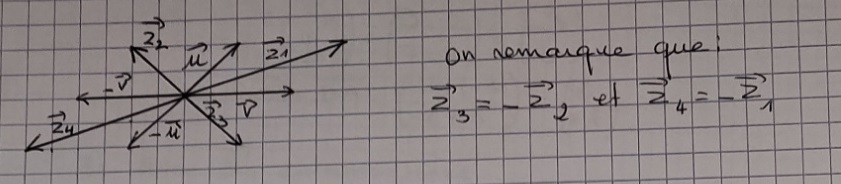
Fiche d'exercices n°2 : notations des vecteurs
à l'aide des points
Correction
Fiche d'exercice n°1 : notion de vecteur
Rappels de troisième
Rappels de collège sur
les fractions
Exemples d'application
Exercice 53 page 51
Enoncé
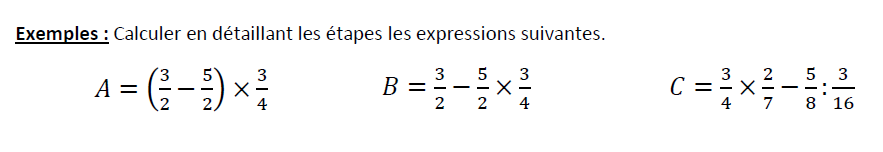
Correction
Enoncé
Correction
